【机器学习】算法原理详细推导与实现(五):支持向量机(下)

精选 0 956

小小草 2020年8月23日 08:38 发表

摘要：上一章节介绍了支持向量机的生成和求解方式，能够根据训练集依次得出ωω、bb的计算方式，但是如何求解需要用到核函数，将在这一章详细推导实现。

上一章节介绍了支持向量机的生成和求解方式，能够根据训练集依次得出 $ω$ 、 $b$ 的计算方式，但是如何求解需要用到核函数，将在这一章详细推导实现。

核函数

在讲核函数之前，要对上一章节得到的结果列举出来。之前需要优化的凸函数为：

m i n_{γ, ω, b} - > \frac{1}{2} | | ω | |^{2}

y^{(i)} (ω^{T} x^{(i)} + b) \geq 1, i = 1, 2, . . ., m

这里假设数据是线性可分隔的，对于这个优化项目，给定一个训练集合，这个问题的算法会找到一个数据集合的最优间隔分类器，可以使训练样本的几何间隔最大化。

在上一章节【机器学习】算法原理详细推导与实现(四):支持向量机(上)中，我们推出了这个问题的对偶问题，也就是要使这个式子最大化：

m a x_{α} Γ (ω, b, α) = \sum_{i = 1}^{m} α_{i} - \frac{1}{2} \sum_{i = 1, j = 1}^{m} α_{i} α_{j} y^{(i)} y^{(j)} < x^{(i)}, x^{(j)} >

α_{i} \geq 0, i = 1, 2, . . ., m

\sum_{i = 1}^{m} α_{i} y^{(i)} = 0

上面是我们的原始问题，且根据拉格朗日对偶步骤计算得到参数 $ω$ ：

ω = \sum_{i = 1}^{m} α_{i} y^{(i)} x^{(i)}

b = \frac{m a x_{i : y^{(i)} = - 1} ω^{T} x^{(i)} + m i n_{i : y^{(i)} = 1} ω^{T} x^{(i)}}{2}

当需要做分类预测时，需要对新来的输入值 $x$ 进行计算，计算其假设的值是否大于零，也就是做一次线性运算来判断是正样本还是负样本，有如下计算函数：

\begin{aligned} h_{ω, b} (x) & = g (ω^{T} x + b) \\ = g (\sum_{i = 1}^{m} α_{i} y^{(i)} < x^{(i)}, x > + b) \end{aligned}

核函数概念

接下来要介绍“核”的概念，这个概念具有这样的性质：

算法对于x的依赖仅仅局限于这些内积的计算，甚至在整个算法中，都不会直接使用到向量x的值，而是只需要用到训练样本与输入特征向量的内积

而“核”的概念是这样的，考虑到最初在【机器学习】算法原理详细推导与实现(一):线性回归中提出的问题，比如有一个输入 $x \in R$ 是房屋的面积， $y$ 是房子的价格。假设我们从样本点的分布中看到 $x$ 和 $y$ 符合3次曲线，那么我们会希望使用 $x$ 的三次多项式来逼近这些样本点。首先将特征 $x$ 扩展到三维 $(x, x^{2}, x^{3})$ ，这里将这种特征变换称作特征映射，映射函数为 $φ (x)$ ：

φ (x) = [\begin{matrix} x \\ x^{2} \\ x^{3} \end{matrix}]

用 $φ (x)$ 代表原来的特征 $x$ 映射成的，这里希望得到映射后的特征应用于svm分类，而不是最初的一维特征，只需要将前面 $ω^{T} x + b$ 公式中的内积从 $< x^{(i)}, x^{(j)} >$ 映射到 $< φ (x)^{(i)}, φ (x)^{(j)} >$ 。至于为什么需要映射后的特征而不是最初的特征来参与计算，上面提到的一个原因：为了更好的拟合，另外一个原因是样本可能存在线性不可分的情况，而特征映射到高维过后往往就可分了。

如果原始特征的内积为 $< x, z >$ ，映射后为 $< φ (x), φ (z) >$ ，那么一般核函数定义为：

K (x, z) = φ (x)^{T} φ (z)

为什么会那么定义核函数？有些时候 $φ (x)$ 的维度将会非常的高，可能会包含非常高维的多项式特征，甚至会到无限维。当 $φ (x)$ 的维度非常高时，可能无法高效的计算内积，甚至无法计算。如果要求解前面所提到的凸函数，只需要先计算 $φ (x)$ ，然后再计算 $φ (x)^{T} φ (z)$ 即可，但是这种常规方法是很低效的，比如最开始的特征是 $n$ 维，并将其映射到 $n^{2}$ 维度，这时候计算需要 $O (n^{2})$ 的时间复杂度。这里假设 $x$ 和 $z$ 都是 $n$ 维的：

K (x, z) = (x^{T} z)^{2}

展开后得到：

\begin{aligned} K (x, z) & = (x^{T} z)^{2} \\ = (\sum_{i = 1}^{n} x_{i} z_{i}) (\sum_{j = 1}^{n} x_{j} z_{j}) \\ = \sum_{i = 1}^{n} \sum_{j = 1}^{n} x_{i} x_{j} z_{i} z_{j} \\ = \sum_{i = 1}^{n} \sum_{j = 1}^{n} (x_{i} x_{j}) (z_{i} z_{j}) \\ = φ (x)^{T} φ (z) \end{aligned}

也就是说，如果开始的特征是 $n$ 维，并将其映射到 $n^{2}$ 维度后，其映射后的计算量为 $O (n^{2})$ 。而如果只是计算原始特征 $x$ 和 $z$ 的内积平方，时间复杂度还是 $O (n)$ ,其结果等价于映射后的特征内积。

回到之前的假设，当 $n = 3$ 时，这个核 $K (x, z)$ 对应的特征映射 $φ (x)$ 为：

φ (x) = [\begin{matrix} x_{1} x_{1} \\ x_{1} x_{2} \\ x_{1} x_{3} \\ x_{2} x_{1} \\ x_{2} x_{2} \\ x_{2} x_{3} \\ x_{3} x_{1} \\ x_{3} x_{2} \\ x_{3} x_{3} \end{matrix}]

这是时间复杂度为 $O (n^{2})$ 计算方式，而如果不计算 $φ (x)$ ，直接计算 $< x, z >$ 从而得到< $φ (x)$ , $φ (z)$ >的内积，时间复杂度将缩小 $O (n)$ 。

同理将核函数定义为：

\begin{aligned} K (x, z) & = (x^{T} z + c) \\ = \sum_{i, j = 1}^{n} (x_{i} x_{j}) (z_{i} z_{j}) + \sum_{i = 1}^{n} (\sqrt{2 c x_{i}}) (\sqrt{2 c x_{j}}) + c^{2} \end{aligned}

当 $n = 3$ 时，这个核 $K (x, z)$ 对应的特征映射 $φ (x)$ 为：

φ (x) = [\begin{matrix} x_{1} x_{1} \\ x_{1} x_{2} \\ x_{1} x_{3} \\ x_{2} x_{1} \\ x_{2} x_{2} \\ x_{2} x_{3} \\ x_{3} x_{1} \\ x_{3} x_{2} \\ x_{3} x_{3} \\ \sqrt{2 c} x_{1} \\ \sqrt{2 c} x_{2} \\ \sqrt{2 c} x_{3} \\ c \end{matrix}]

总结来说，核的一种一般化形式可以表示为：

K (x, z) = (x^{T} z + c)^{d}

对应着 $[\begin{matrix} n + d \\ d \end{matrix}]$ 个特征单项式，即特征维度。

假如给定一组特征 $x$ ，将其转化为一个特征向量 $φ (x)$ ;给定一组特征 $z$ ，将其转化为一个特征向量 $φ (z)$ ，所以核计算就是两个向量的内积 $< φ (x), φ (z) >$ 。如果 $φ (x)$ 和 $φ (z)$ 向量夹角越小，即两个向量越相似(余弦定理)，那么 $φ (x)$ 和 $φ (z)$ 将指向相同的方向，因此内积会比较大；相反的如果 $φ (x)$ 和 $φ (z)$ 向量夹角越大，即两个向量相似度很低，那么 $φ (x)$ 和 $φ (z)$ 将指向不同的方向，因此内即将会比较小。

如果有一个核函数如下:

K (x, z) = e x p^{(- \frac{| | x - z | |^{2}}{2 σ^{2}})}

在前面说了：为什么需要映射后的特征而不是最初的特征来参与计算？

上面提到了两个原因：

为了更好的拟合
样本可能存在线性不可分的情况，而特征映射到高维过后往往就可分了

第二种情况如下所示：

左边使用线性的时候，使用svm学习出 $ω$ 和 $b$ 后，新来样本 $x$ 就可以代入到 $ω^{T} x + b$ 中进行判断，但是像图中所示是无法判断的；如果使用了核函数过后， $ω^{T} x + b$ 变成了 $ω^{T} φ (x) + b$ ，直接可以用下面的方式计算：

\begin{aligned} ω^{T} x + b & = (\sum_{i = 1}^{m} α_{i} y^{(i)} x^{(i)})^{T} x + b \\ = \sum_{i = 1}^{m} α_{i} y^{(i)} < x^{(i)}, x > + b \\ = \sum_{i = 1}^{m} α_{i} y^{(i)} K (x^{(i)}) + b \end{aligned}

只需要将 $< x^{(i)}, x >$ 替换成 $K (x^{(i)})$ 就能将低维特征转化为高维特征，将线性不可分转化成高维可分。

规则化和不可分情况处理

我们之前讨论的情况都是建立在样例线性可分的假设上，当样例线性不可分时，我们可以尝试使用核函数来将特征映射到高维，这样很可能就可分了。然而，映射后我们也不能100%保证可分。那怎么办呢，我们需要将模型进行调整，以保证在不可分的情况下，也能够尽可能地找出分隔超平面。

看下面的图可以解释：

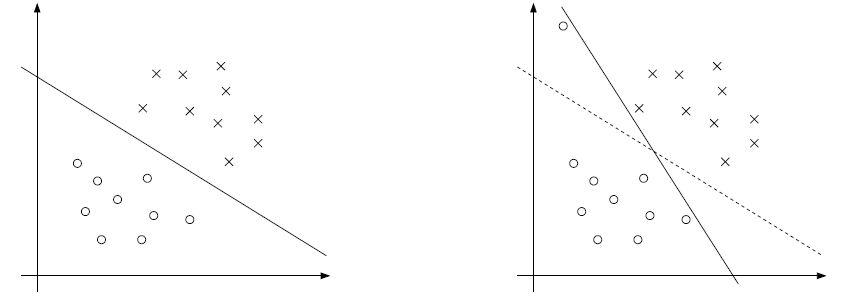
在右边的图可以可以看到上面一个离群点（可能是噪声），会造成超平面的移动改变，使集合间隔的间隔距离缩小，可见以前的模型对噪声非常敏感。再有甚者，如果离群点在另外一个类中，那么这时候就是线性不可分了。这时候我们应该允许一些点游离在模型中违背限制条件（函数间隔大于 1）。我们设计得到新的模型如下（也称软间隔）：

m i n_{γ, ω, b} - > \frac{1}{2} | | ω | |^{2} + C \sum_{i = 1}^{m} ξ_{i}

y^{(i)} (ω^{T} x^{(i)} + b) \geq 1 - ξ_{i}, i = 1, 2, . . ., m

ξ_{i} \geq 0, i = 1, . . ., m

引入非负参数 $ξ_{i}$ (松弛变量)过后，也就意味着允许某些样本的函数间隔小于1，甚至是负数，负数就代表样本点在对方区域中，如上方右边图的虚线作为超平面，一个空心圆点的函数间隔为负数。

增加新的条件后，需要重新调整目标函数，增加对离群点进行处罚，也就是在求最小值的目标函数后面加上 $C \sum_{i = 1}^{m} ξ_{i}$ ，因为定义 $ξ_{i} \geq 0$ ，所以离群点越多，那么目标函数的值越大，就等于违背求最小值的初衷。而 $C$ 是离群点的权重， $C$ 越大表明离群点对于目标函数的影响越大，也就是越不希望看到离群点。

修改目标函数后，原式子变成：

Γ (ω, b, ξ, α, r) = \frac{1}{2} ω^{T} ω + C \sum_{i = 1}^{m} ξ_{i} - \sum_{i = 1}^{m} α_{i} [y^{(i)} (x^{T} ω + b) - 1 + ξ_{i}] - \sum_{i = 1}^{m} r_{i} ξ_{i}

这里的 $α$ 和 $r$ 都是拉格朗日算子，根据上一章节拉格朗日的求解步骤：

构造出拉格朗日函数后，将其看作是变量 $ω$ 和 $b$ 的函数
分别对其求偏导，得到 $ω$ 和 $b$ 的表达式
然后带入上述拉格朗日式子中，求带入后式子的极大值

最后化简得到的结果是：

m a x_{α} W (α) = \sum_{i = 1}^{m} α_{i} - \frac{1}{2} \sum_{i = 1, j = 1}^{m} α_{i} α_{j} y^{(i)} y^{(j)} < x^{(i)}, x^{(j)} >

C \geq α_{i} \geq 0, i = 1, 2, . . ., m

\sum_{i = 1}^{m} α_{i} y^{(i)} = 0

这里唯一不同的地方是限制条件多了一个离群点的权重 $C$ 。

SMO优化算法

SMO 是一个求解对偶问题的优化算法，目前还剩下最后的对偶问题还未解决：

m a x_{α} W (α) = \sum_{i = 1}^{m} α_{i} - \frac{1}{2} \sum_{i = 1, j = 1}^{m} α_{i} α_{j} y^{(i)} y^{(j)} < x^{(i)}, x^{(j)} >

C \geq α_{i} \geq 0, i = 1, 2, . . ., m

\sum_{i = 1}^{m} α_{i} y^{(i)} = 0

我们需要根据上述问题设计出一个能够高效解决的算法，步骤如下：

首先选择两个要改变的 $α$ 值 $α_{i}$ 、 $α_{j}$
其次保持除了 $α_{i}$ 、 $α_{j}$ 之外的所有参数固定
最后同时相对于这两个参数使 $ω$ 取最优，且同时满足所有约束条件

怎样在满足所有约束条件的情况下，相对于选出来的两个参数 $α_{i}$ 、 $α_{j}$ 使 $ω$ 取最优值？SMO优化算法能够高效完成这个工作。SMO算法非常的高效，只需要更多次数的迭代以达到收敛，而且每次迭代所需要的代价都非常小。

为了推出这个步骤，我们需要相对于 $α_{i}$ 、 $α_{j}$ 进行更新，假设取值是 $α_{1}$ 、 $α_{2}$ ，即假设 $α_{1}$ 、 $α_{2}$ 不再是变量（可以由其他值推出），可以根据约束条件推导得到：

\begin{aligned} \sum_{i = 1}^{m} α_{i} y^{(i)} & = 0 \\ α_{1} y_{1} + α_{2} y_{2} & = - \sum_{i = 3}^{m} α_{i} y^{(i)} \end{aligned}

由于 $α_{3}$ 、 $α_{4}$ 、...、 $α_{m}$ 都是已知固定值，因此为了方便将等式右边，可将等式右边标记成 $ζ$ ：

α_{1} y^{(1)} + α_{2}^{(2)} = ζ

还有一个约束条件：

C \geq α_{i} \geq 0, i = 1, 2, . . ., m

这个约束条件被称作为“方形约束”，如果将 $α_{1}$ 、 $α_{2}$ 画出来：

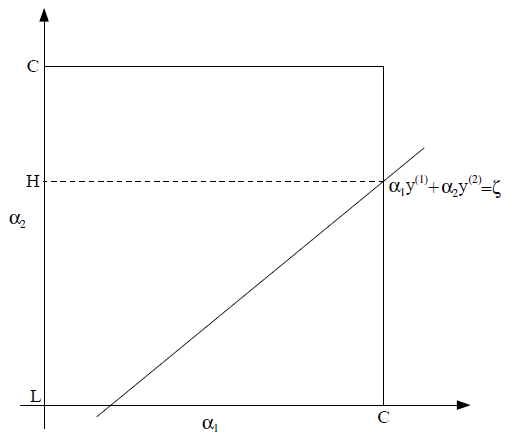
那么 $α_{1}$ 、 $α_{2}$ 表示的值应该都在 $[0, C]$ 之间，也就是在方框里面，这意味着：

α = \frac{ζ - α_{2} y^{(2)}}{y^{(1)}}

然后带入到需要求解的式子中：

W (α_{1}, α_{2}, . . ., α_{m}) = W (\frac{ζ - α_{2} y^{(2)}}{y^{(1)}}, α_{2}, . . ., α_{m})

在前面我们认为 $α_{3}$ 、 $α_{4}$ 、...、 $α_{m}$ 都是已知固定值，只有 $α_{1}$ 、 $α_{2}$ 是未知需要求解的。那么把 $W (\frac{ζ - α_{2} y^{(2)}}{y^{(1)}}, α_{2}, . . ., α_{m})$ 展开后可以表示成 $a α_{2}^{2} + b α_{2} + c$ 的形式，其中 $a$ 、 $b$ 、 $c$ 是由 $α_{3}$ 、 $α_{4}$ 、...、 $α_{m}$ 表示出来，即 $W$ 是一个二次函数。而其实对于所有的 $α$ ，如果保持其他参数都固定的话，都可以表示成 $W$ 关于某个 $α$ 的一元二次函数：

\begin{aligned} W (α_{1}, α_{2}, . . ., α_{m}) & = W (\frac{ζ - α_{2} y^{(2)}}{y^{(1)}}, α_{2}, . . ., α_{m}) \\ = a α_{2}^{2} + b α_{2} + c \end{aligned}

由于上面式子是一个标准的一元二次函数，所以很容易求解出最优值，从而可以得到 $α_{2}$ 的最优值，而这个最优值一定会在上图中 $α_{1} - α_{2} = ζ$ 这条线上，且在“方形约束”中。按照这种方式解除 $α_{2}$ 后，之后根据 $α_{1}$ 和 $α_{2}$ 的关系求解出 $α_{1}$ ，这样子就求解出了相对于 $α_{1}$ 和 $α_{2}$ 关于 $W$ ，且满足所有约束条件的最优值，该算法的关键是对一个一元二次函数求最优解，这个求解非常简单，这就使得SMO算法的内嵌计算非常高效。

如何求解 $α_{2}$ 的值呢？只需要对式子进行求导 $a α_{2}^{2} + b α_{2} + c$ ，即对 $W$ 进行求导，然而要保证 $α_{2}$ 即在方形约束内，也在 $α_{1} - α_{2} = ζ$ 这条线上，那么就要保证 $H \geq α_{2} \geq L$ ，这里使用 $α_{2}^{n e w, u n c l i p p e d}$ 来表示求导出来的 $α_{2}$ ，然后最后 $α_{2}^{n} e w$ 的迭代更新方式如下所示：

α_{2}^{n} e w = {\begin{cases} H, & if α_{2}^{n e w, u n c l i p p e d} > H \\ α_{2}^{n e w, u n c l i p p e d}, & if H \geq α_{2}^{n e w, u n c l i p p e d} \geq L \\ L, & if α_{2}^{n e w, u n c l i p p e d} < L \end{cases}

得到 $α_{2}$ 后，由此可以返回求解 $α_{1}$ 得到新值 $α_{1}$ ，这里就是SMO优化算法的核心思想。根据SMO优化算法的核心思想：

首先选择两个要改变的 $α$ 值 $α_{i}$ 、 $α_{j}$
其次保持除了 $α_{i}$ 、 $α_{j}$ 之外的所有参数固定
最后同时相对于这两个参数使 $ω$ 取最优，且同时满足所有约束条件

可以求解出所有的 $α$ ，使得 $W$ 取得最大值，即原问题将得到解决：

m a x_{α} W (α) = \sum_{i = 1}^{m} α_{i} - \frac{1}{2} \sum_{i = 1, j = 1}^{m} α_{i} α_{j} y^{(i)} y^{(j)} < x^{(i)}, x^{(j)} >

C \geq α_{i} \geq 0, i = 1, 2, . . ., m

\sum_{i = 1}^{m} α_{i} y^{(i)} = 0

总结

svm的步骤总结如下：

先确定间隔器，这里svm一般默认是几何间隔
由间隔器确定间隔函数
从间隔函数查看是否包含不等式约束形式
根据拉格朗日对偶步骤计算得到参数w、b
规则化不可分的参数，即在原对偶式子中加入离群点权重 $C$ ，问题转换为 $m a x_{α} W (α)$
利用SMO优化算法求解 $W (α)$ 最优值，首先选择两个要改变的 $α$ 值 $α_{i}$ 、 $α_{j}$
其次保持除了 $α_{i}$ 、 $α_{j}$ 之外的所有参数固定
最后同时相对于这两个参数使 $ω$ 取最优，且同时满足所有约束条件，最后确定选取的这两个 $α_{i}$ 、 $α_{j}$ 的值
重复步骤6-9直到所有参数 $α$ 求解完成

svm在神经网络出来之前一直是最优的算法。相比于之前的算法推导复杂一些，但是逻辑并不难，它不想逻辑回归那样去拟合样本点，而是根据几何空间去寻找最优的分割超平面，为了判断哪个超平面最好，引入几个平面间隔最大化目标，从而求解出结果。

实例

有一份数据svm_data1，加载读取：

import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat
from sklearn import svm

# 加载data1
raw_data = loadmat('./svm_data1.mat')
# print(raw_data)

# 读取data1的数据
data = pd.DataFrame(raw_data['X'], columns=['X1', 'X2'])
data['y'] = raw_data['y']

positive = data[data['y'].isin([1])]
negative = data[data['y'].isin([0])]
print(positive.shape)
print(negative.shape)

# 查看data1的数据分布
fig, ax = plt.subplots(figsize=(12, 8))
ax.scatter(positive['X1'], positive['X2'], s=50, marker='x', label='Positive')
ax.scatter(negative['X1'], negative['X2'], s=50, marker='o', label='Negative')
ax.legend()
plt.show()

数据分布如下所示：

可以看到数据分在两边很好区分，用一般的分类器例如逻辑回归、朴素贝叶斯即可区分，这里就用svm的线性核进行分类，设置离群点的权重 $C = 1$ ，即不区分离群点：

svc = svm.LinearSVC(C=1, loss='hinge', max_iter=1000)

svc.fit(data[['X1', 'X2']], data['y'])
data1_score_1 = svc.score(data[['X1', 'X2']], data['y'])
print(data1_score_1)

得到的准确率为0.980392156863，分类的图如下：

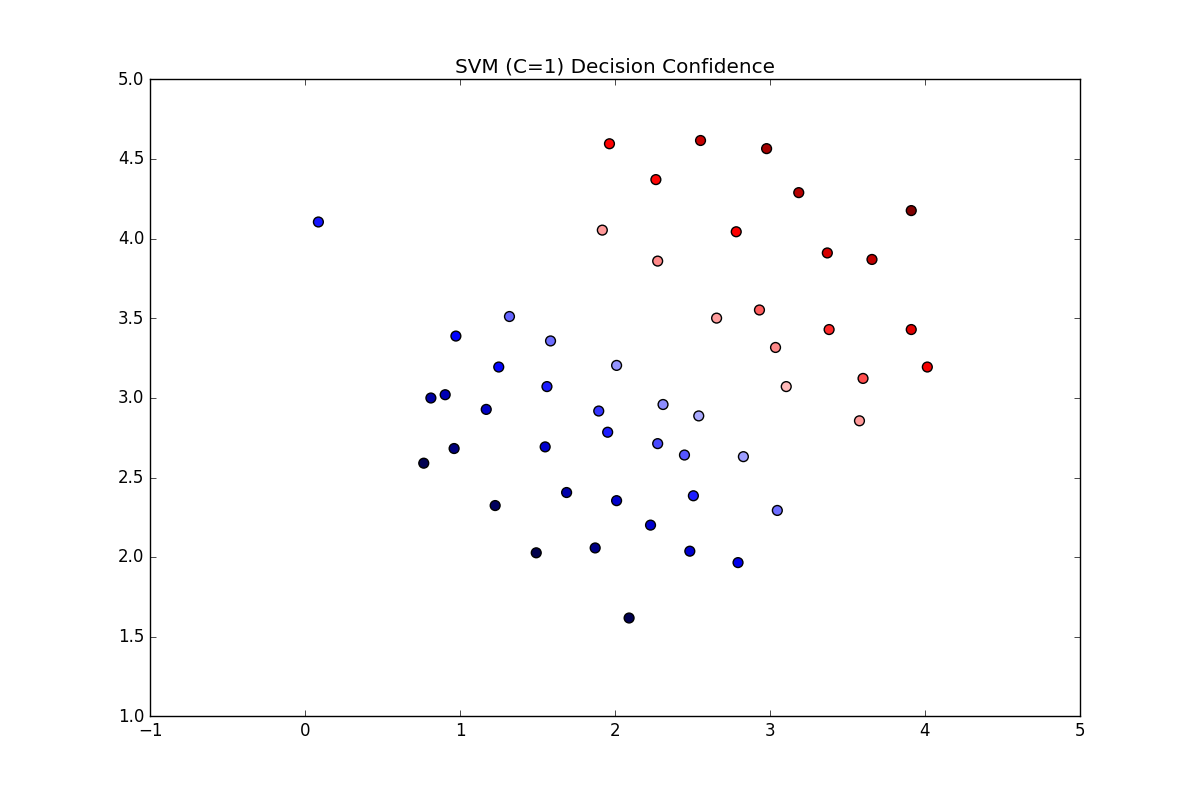
可以看到左上角有一个点原来是正样本，但是被分类为蓝色(负样本)，所以正样本21个，负样本30个，被误分的概率刚好是 $\frac{1}{51} = ‭ 0.01960784313 ‬$ ，所以准确率是 $1 - ‭ 0.01960784313 ‬ = 0.980392156863$ ，刚好对的上。现在这里设置离群点的权重 $C = 100$ 用以区分离群点，得到的准确率为1.0，分类图像为：

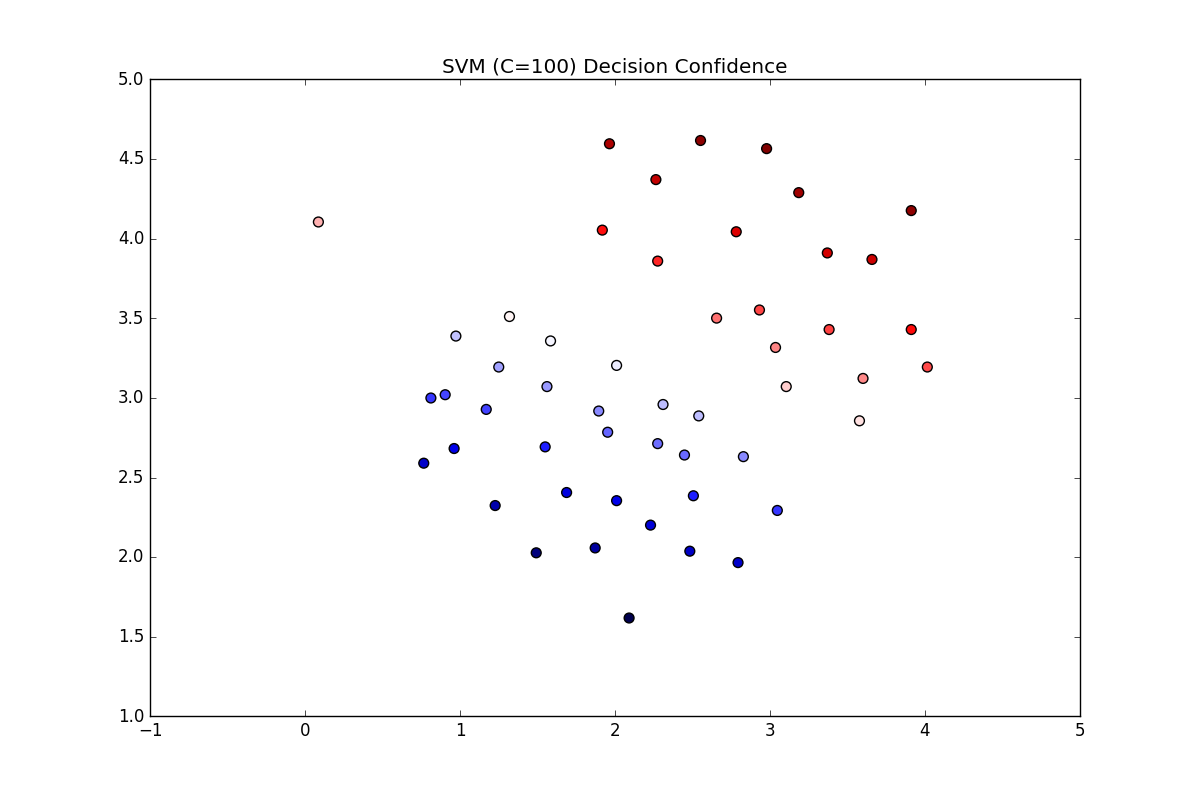
再看第二份数据分布图如下：

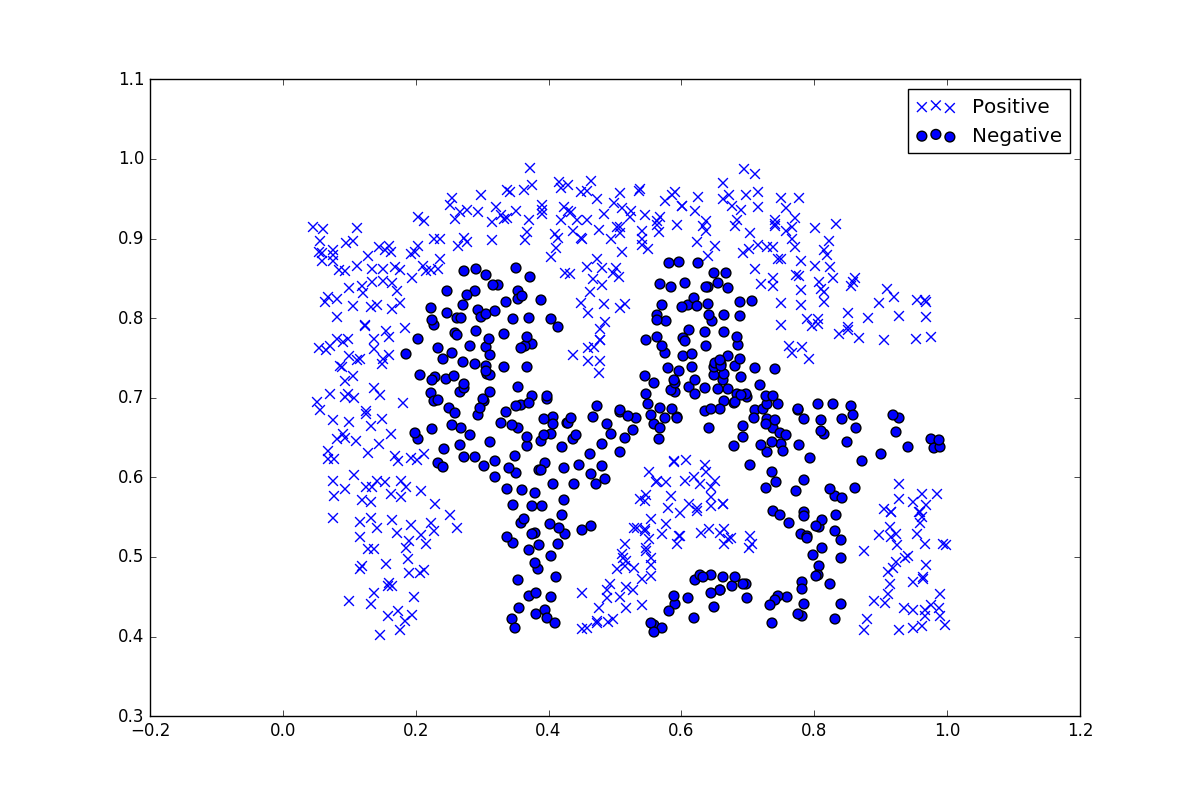
这次就不能用线性核分类，需要用到RBF核分类：

# 做svm分类，使用RBF核
svc = svm.SVC(C=100, gamma=10, probability=True)
svc.fit(data[['X1', 'X2']], data['y'])
data['Probability'] = svc.predict_proba(data[['X1', 'X2']])[:, 0]

分类的结果图如下所示：

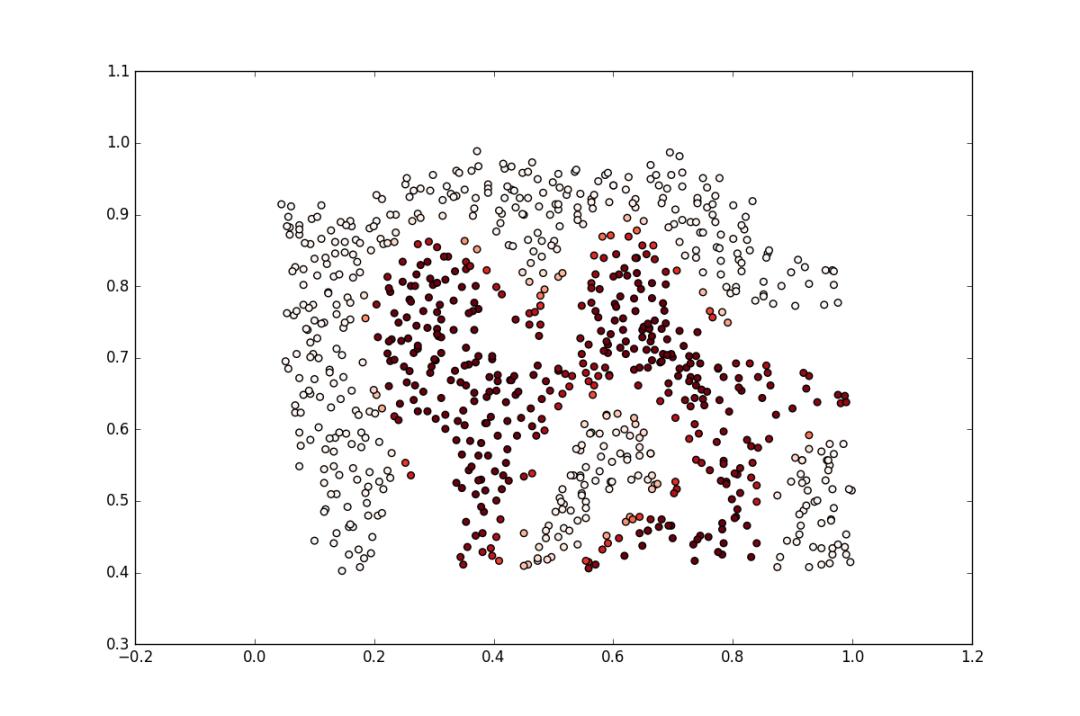
结果得到的准确率只有0.769228287521，因此设置了网格调参：

# 简单的网格调参
C_values = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]
gamma_values = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]

best_score = 0
best_params = {'C': None, 'gamma': None}

# 网格调参开始
for C in C_values:
    for gamma in gamma_values:

        # 做svm分类，使用RBF核
        svc = svm.SVC(C=C, gamma=gamma, probability=True)
        svc.fit(data[['X1', 'X2']], data['y'])

        # 交叉验证
        data2_score = cross_validation.cross_val_score(svc, data[['X1', 'X2']], data['y'], scoring='accuracy', cv=3)
        print(data2_score.mean())

最后准确率提高到0.858437379017，调整到的最优参数为{'C': 10, 'gamma': 100}

点赞 0 收藏(0)