何恺明等降维打击！彻底颠覆AI生图，无需预训练

新智元报道

编辑：KingHZ

【新智元导读】何恺明团队又一力作！这次他们带来的是「生成模型界的降维打击」——MeanFlow：无需预训练、无需蒸馏、不搞课程学习，仅一步函数评估（1-NFE），就能碾压以往的扩散与流模型！

何恺明有新论文了！

全新的生成模型MeanFlow，最大亮点在于它彻底跳脱了传统训练范式——无须预训练、蒸馏或课程学习，仅通过一次函数评估（1-NFE）即可完成生成。

MeanFlow在ImageNet 256×256上创下3.43 FID分数，实现从零开始训练下的SOTA性能。

图1（上）：在ImageNet 256×256上从零开始的一步生成结果

在ImageNet 256×256数据集上，MeanFlow在一次函数评估（1-NFE）下达到了3.43的FID分数，性能相比此前同类最佳方法有50%到70%的相对提升（见图1左）。

此外，MeanFlow训练过程从零开始，无需预训练、蒸馏或课程学习。

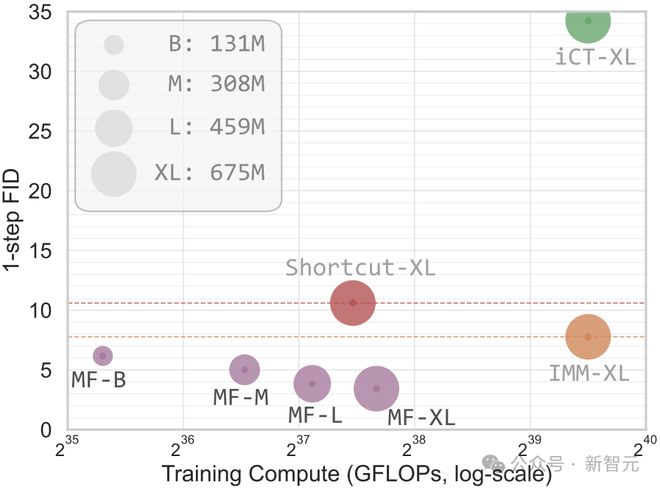
图1（左）：算力和一次函数评估FID分数

其中iCT、Shortcut和MF都是一次函数评估（1-NFE），而IMM则使用了两次函数评估（2-NFE）的引导策略。

具体数值见表2。

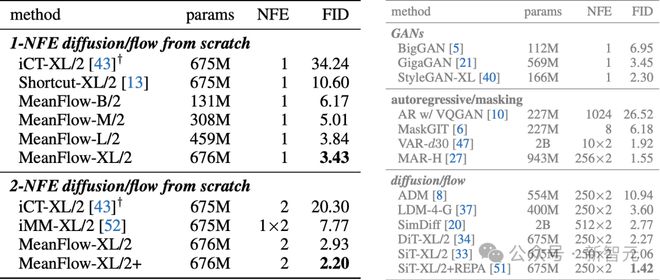
表2：ImageNet-256×256上的类别条件生成实验，不同模型的参数、FID得分等统计数据

值得一提的是，作者共有5位，其中4位是华人，均来自CMU和MIT两所顶校。

其中一作耿正阳，是CMU的博士生，在MIT访问时完成了这次研究的部分工作。

论文链接：https://arxiv.org/abs/2505.13447

在新论文中，研究者提出了系统且高效的一步生成建模框架MeanFlow。

传统Flow Matching依赖建模瞬时速度场，而MeanFlow首创性地引入平均速度场（Mean Velocity Field）这一概念。

平均速度是指「位移/时间间隔」的比值，本质上是对瞬时速度在时间轴上的积分。

仅基于这一定义，研究者推导出了平均速度与瞬时速度之间清晰且内在的数学关系，这为神经网络训练提供了理论依据。

在这一基本概念之上，直接训练神经网络，对平均速度场建模。

为此，研究者设计了新的损失函数，引导网络去满足平均速度与瞬时速度之间的内在关系，无需引入额外的启发式方法。

由于存在明确定义的目标速度场，理论上最优解与网络的具体结构无关，这种属性有助于训练过程更加稳健和稳定。

此外，新方法还能自然地将「无分类器引导」（Classifier-Free Guidance，CFG）融入目标速度场，在采样阶段使用引导时不会带来额外的计算开销。

详细结果

在图1和表2（左侧）中，研究者将MeanFlow与现有的一步扩散/流模型进行了比较。

总体来看，MeanFlow在同类方法中表现显著优越：

• 新模型在ImageNet 256×256上实现了3.43的FID分数，相比IMM的7.77，相对提升超过50%；

• 如果仅比较1-NFE（一次函数评估）的生成结果，MeanFlow相比此前的最优方法Shortcut（FID 10.60），相对提升接近70%。

这表明，MeanFlow在很大程度上缩小了一步与多步扩散/流模型之间的性能差距。

在2-NFE（两次函数评估）设定下，新方法取得了2.20的FID分数（见表2左下角）。

这个结果已经可以媲美许多多步方法的最优基线。

它们都采用了XL/2级别的骨干网络，且NFE达到250×2（见表2右侧）。

这进一步表明，少步数的扩散/流模型已经具备挑战多步模型的潜力。

此外，未来还能进一步提升性能。

图5：1-NFE生成结果示例

在CIFAR-10数据集（32×32）上，研究人员进行了无条件生成实验，结果列在表3中。

使用1-NFE采样时，他们使用FID-50K分数作为性能指标。

所有方法均采用相同的U-Net架构（约5500万参数）。

需要注意的是，其他所有对比方法均使用了EDM风格的预处理器（pre-conditioner），而新方法没有使用任何预处理器。

在CIFAR-10这个数据集上，新方法在性能上与现有方法具有竞争力。

表3：CIFAR-10无条件生成结果

前身：流匹配

流匹配（Flow Matching，简称FM）是一种生成建模范式。

Flow Matching将「连续归一化流」（Continuous Normalizing Flows，CNFs）与「扩散模型」（Diffusion Models，DMs）的一些关键思想相结合，从而缓解了这两类方法各自存在的核心问题。

形式上，给定数据x∼pdata(x)和先验噪声ϵ∼pprior(ϵ)，可以构造一条流动路径，

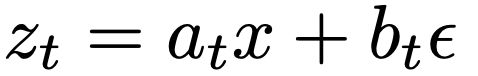
其中t表示时间，a_t和b_t是预设的调度函数。

路径的速度定义为

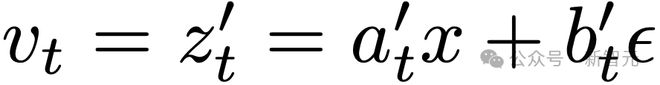
这个速度被称为条件速度（conditional velocity）。参见图2左侧部分。

Flow Matching本质上是在对所有可能情况的期望进行建模，这种平均后的速度称为边缘速度（marginal velocity）（见图2右侧）：

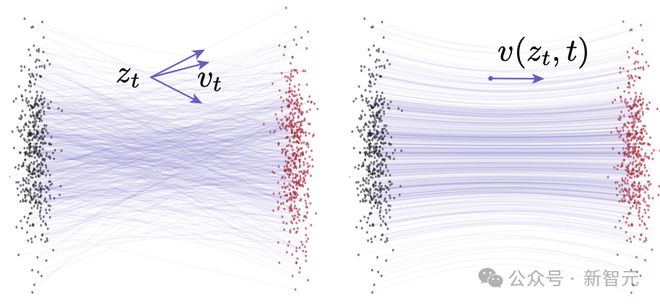
图2：Flow Matching中的速度场示意图。左图：条件流（ConditionalFlows）。同一个z_t可能由不同的(x,ϵ)组合生成，因此会对应不同的条件速度v_t。右图：边缘流（Marginal Flows）。通过对所有可能的条件速度进行边缘化（求平均）得到边缘速度场。这个边缘速度场被作为训练神经网络时的「真实目标速度场」

图例说明：灰点表示从先验分布中采样得到的样本，红点表示来自真实数据分布的样本。

接着，学习由参数θ表示的神经网络v_θ，来拟合这个边缘速度场，其损失函数为：

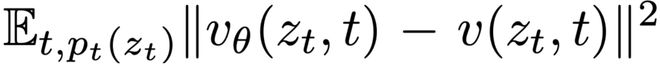
但由于式(1)中的边缘化过程难以直接计算，因此Flow Matching提出使用条件Flow Matching损失来代替：

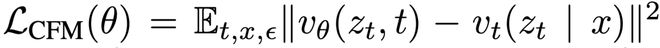
其中目标速度v_t是条件速度。

可以证明，最小化上述两个损失函数是等价的。

一旦得到了边缘速度场v(z_t,t)，就可以通过求解下面的常微分方程（ODE）来生成样本：

初始值为z_1=ϵ，上述微分方程的解可以写成积分形式：

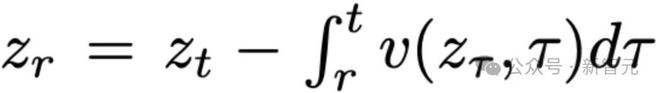
其中r表示另一个时间点。

在实际中，这个积分通常通过数值方法在离散时间步上进行近似。

值得注意的是，即便条件流被设计为「直线流动」（即所谓「校正流」），最终得到的边缘速度场（公式(1)）往往仍会诱导出弯曲的轨迹（见图2的示意）。

这种轨迹的弯曲不仅仅是因为神经网络的近似误差，更是源于真实的边缘速度场本身。

当对这些弯曲轨迹使用粗粒度的时间离散化时，数值ODE解法往往会产生较大的误差，从而导致生成结果不准确。

MeanFlow模型

平均流（Mean Flows）的核心思想是：引入一个表示平均速度的新场（velocity field），而传统Flow Matching所建模的是瞬时速度。

平均速度定义

平均速度被定义为两个时间点t和r之间的位移（通过对瞬时速度积分获得），再除以时间间隔。

形式上，平均速度u定义如下：

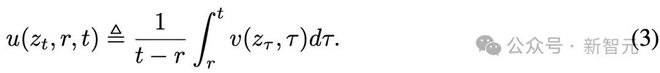
为了突出概念上的区别，统一用u表示平均速度，用v表示瞬时速度。

平均速度场u(z_t，r，t)同时依赖于起始时间r和终止时间t，如图3所示。

图3：平均速度场

需要注意的是，平均速度u本质上是瞬时速度v的泛函结果。

因此，平均速度场是由瞬时速度场决定的，并不依赖于任何神经网络。

从概念上讲，就像在Flow Matching中，瞬时速度v是训练的「真实目标场」，在MeanFlow中，平均速度u则扮演着类似的角色，是学习所依据的「真实速度场」。

MeanFlow模型的最终目标是：用神经网络近似平均速度场。

这样做的优势显著：一旦平均速度被准确建模，就可以仅通过一次前向计算来近似整个流动路径。

换句话说，这种方法非常适合一步或少步数的生成任务，因为它在推理阶段不需要显式计算时间积分——这是传统建模瞬时速度方法所必须的步骤。

不过，在实践中，直接使用公式(3)定义的平均速度作为训练网络的「真值」行不通，因为这要求在训练时就对瞬时速度执行积分，计算成本高且不可行。

研究人员的关键见解是：可以对平均速度的定义公式进行数学变形，从而构造一个更易于训练的优化目标，即使在只能访问瞬时速度的前提下依然可行。

MeanFlow恒等式

为了得到适合训练的形式，平均速度的定义公式(3)被重新改写为：

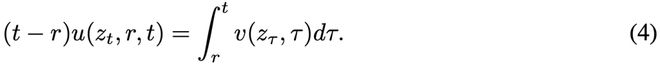
接着，对这个等式的两边关于t求导（把r当作常数），然后运用函数积的求导法则和微积分基本定理，得到：

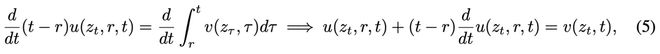
整理上式，即可得到核心的MeanFlow恒等式：

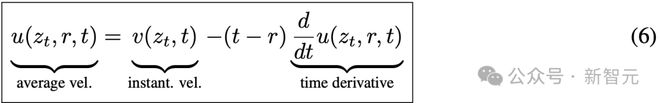
它刻画了平均速度u和瞬时速度v之间的本质联系。

需要说明的是，公式(6)与之前的积分公式(4)是等价的（详见原文附录B.3）。

在MeanFlow恒等式中，公式右侧给出了可以作为训练目标的形式，可以利用它构建损失函数，来训练神经网络预测u(z_t，r，t)。

为了构建这个损失函数，还需要进一步分解其中的时间导数项。

时间导数的计算

要计算公式(6)右侧第二项全导数（total derivative），它可以用偏导数展开如下：

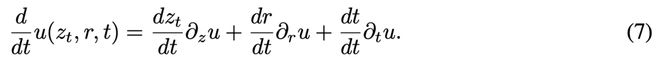
将导数关系带入后得到：

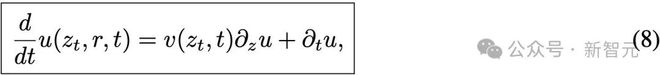
这提供了另一种表达u和v关系的方式。

利用神经网络自动微分，在训练时高效计算时间导数项。

利用平均速度进行训练

到目前为止，上述公式还没有涉及任何网络参数。现在引入可学习的模型u_θ，并希望它满足MeanFlow恒等式（公式(6)）。

研究者定义如下的损失函数来优化网络参数：

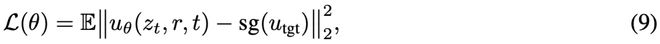
其中，u_tgt是通过MeanFlow恒等式构造的训练目标：

这个目标的几个关键点如下：

• 训练信号来自于瞬时速度v，不需要积分操作，因此相比平均速度定义式(3)更容易实现。

• 虽然公式中出现了对u的偏导数，但实际训练中使用的是网络输出uθ的梯度（自动微分实现）。

• 使用了stop-gradient操作（记为sg）：这是为了避免「二阶反向传播」，从而减小优化的计算负担。

需要说明的是，即使在优化中进行了这些近似，只要u_θ最终能够使损失为零，它就一定满足MeanFlow恒等式，从而也满足最初的平均速度定义。

条件速度替代边缘速度

在公式(10)中的v(z_t，t)是Flow Matching中的边缘速度（见图2右），但它难以直接计算。

因此，借鉴Flow Matching已有的做法，使用条件速度（见图2左）来替代：

这里vt=at′x+bt′ϵ是条件速度，在默认设定下vt=ϵ−x。

论文链接：https://arxiv.org/abs/2210.02747

在算法1中，jvp操作（Jacobian-vector product）非常高效。

使用MeanFlow模型进行采样非常简单：只需将时间积分项替换为平均速度即可，伪代码详见算法2。

带引导的MeanFlow

新方法能够自然支持无分类器引导（Classifier-Free Guidance，CFG）。

与传统做法在采样阶段直接应用CFG不同，研究者将CFG视为底层「真实速度场」的一部分属性。

这种建模方式可以在保留CFG效果的同时，仍保持采样时的1-NFE性能。

构建真实速度场

研究者定义新的带引导的真实速度场vcfg：

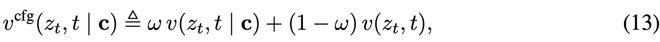
这是一个类别条件场（class-conditional field）与无条件场（class-unconditional field）的线性组合。

其中，类别条件速度（即对给定类别c条件下的边缘速度）、无条件边缘速度，定义如下：

接下来，我们仿照MeanFlow的方式，为vcfg引入对应的平均速度。

根据MeanFlow恒等式（公式6），我们有：

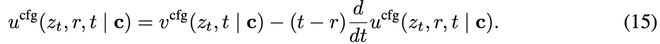
我们再次强调，vcfg和ucfg都是理论上的真实速度场，与神经网络参数无关。

此外，由公式(13)和MeanFlow恒等式导出：

这可以简化计算。

带引导的训练方法

神经网络ucfg,θ来拟合平均速度场，需要构造如下训练目标：

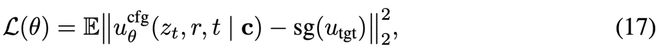
其中目标值为：

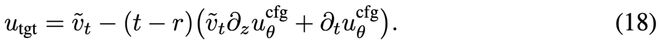
这里的右侧第一项是结合引导权重后的速度定义：

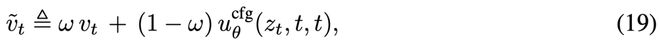
• 其中v_t是样本条件速度，默认设定为vt=ϵ−x。

• 如果ω=1，即纯类别条件引导，则损失函数退化为不含CFG的公式(9)。

• stop-gradient操作用于阻断目标对网络参数的反向传播，避免二阶梯度计算。

此外，为了增强网络对无类别输入的泛化能力，以0%概率随机丢弃类别条件。

单NFE下CFG采样

在本方法中，网络直接学习的是由引导速度vcfg所诱导的平均速度。

因此，在采样阶段，无需再进行线性组合计算，只需直接网络调用即可完成一步采样（见算法2）。

最终，新在保留CFG效果的同时，依然维持了理想的单步采样性能（1-NFE），兼顾了效率与质量。

作者介绍

耿正阳（Zhengyang Geng）

耿正阳，卡内基梅隆大学（CMU）计算机科学博士生。

他热衷于研究动态系统，致力于识别、理解并开发能够自组织形成复杂系统的动态机制。

2020年，他毕业于四川大学，获得计算机科学与技术学士学位。

他在北京大学、Meta等机构实习过多次。

参考资料：

https://arxiv.org/abs/2505.13447

https://mlg.eng.cam.ac.uk/blog/2024/01/20/flow-matching.html